Created Date: 10/5/2015 12:55:02 PM. Two similar objects have corresponding sides 4cm and 7cm. The volume of the larger one is 230 cm 3.What is the volume of the smaller one? Give your answer to 1 decimal place.

A and B are two cylinders that are mathematically similar. The area of the crosssection of

Two cylinders from primary VGP melanomas (H& original magnification… Download Scientific
Solved The two cylinders, A and B, are mathematically similar. The height of cylinder B is
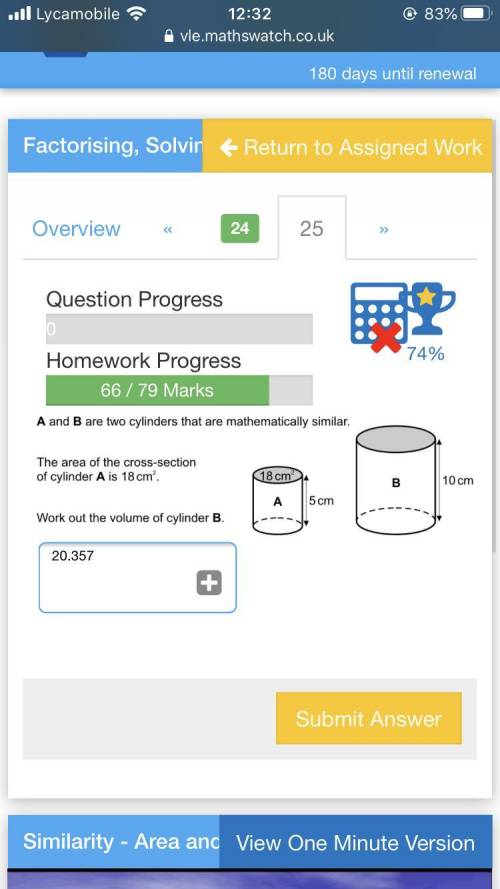
A and and b are two cylinders that are mathematically similar. the area of crosssection of

Similar Shapes (Area and Volume) GCSE maths grade 6
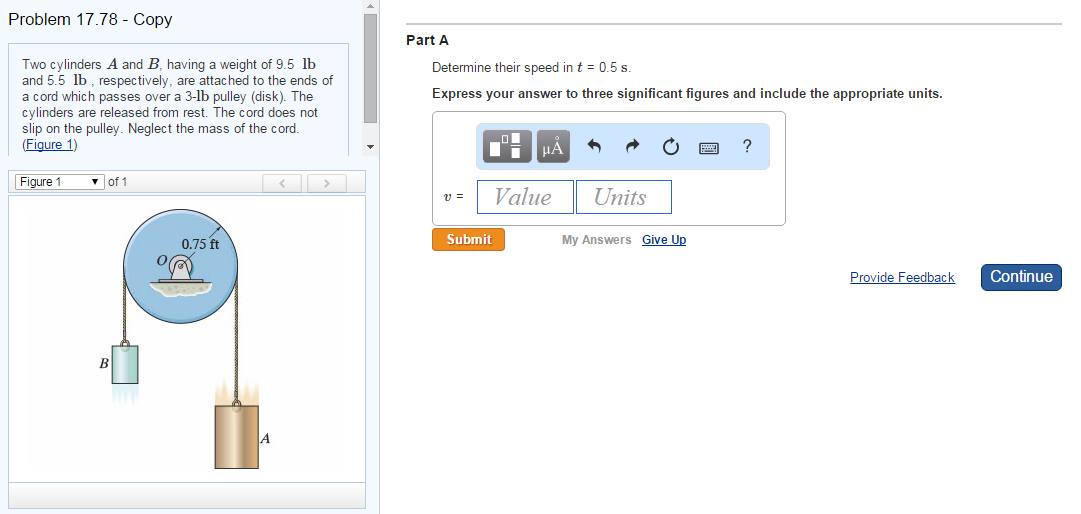
Solved Two cylinders A and B having a weight of 9.5 lb and
Solved The diagram shows two mathematically similar vases, A and B. A has a volume of 405cm^3E
A and B are two cylinders that are mathematically similar. The area of the crosssection of

Cylinders A and B are similar. Cylinder A is 3 times larger than cylinder B. how many times
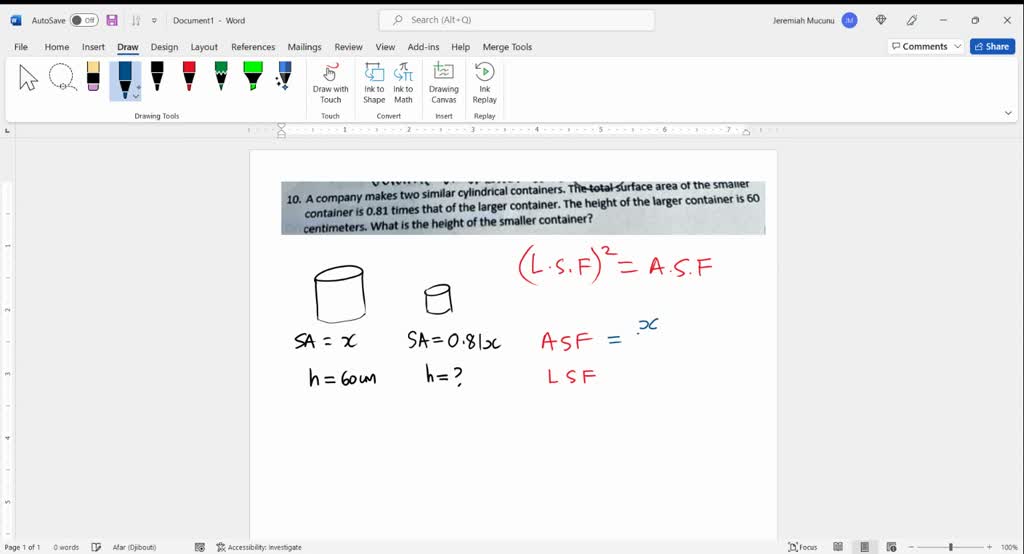
SOLVED Two containers are mathematically similar. Their volumes are 54cm3 and 128 cm3. The

Registration results of two cylinders of an engine block (a) diffusion… Download Scientific
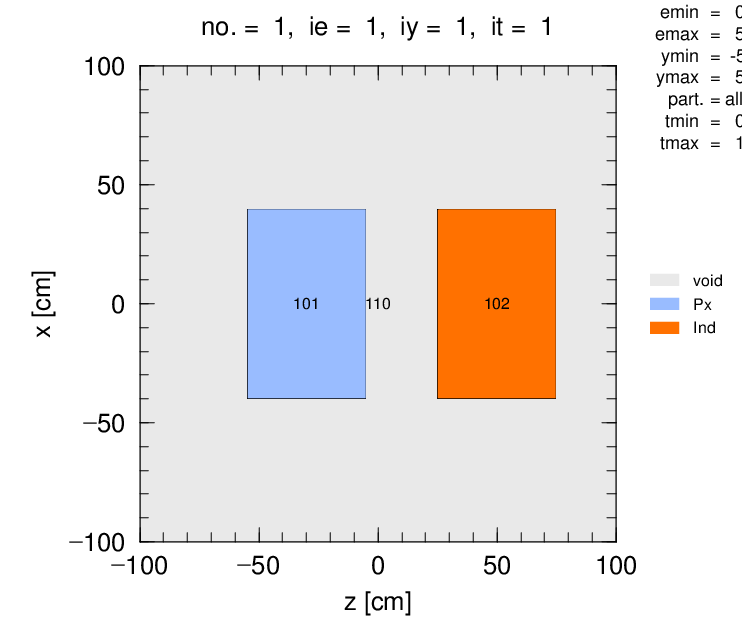
Geometry of two cylinders Questions PHITS Forum

Q19 Answers Paper 4 November 18 OCR GCSE Maths Higher Elevise

A and B are two cylinders that are mathematically similar. The area of the crosssection of

Find the ratio of the volumes of two cylinders with equal heights, if the radius of one is
Solved The shapes below are mathematically similar. Not dra[geometry] Gauthmath

Cylinders A and B have the same radius but different heights. Which statement correctly compares
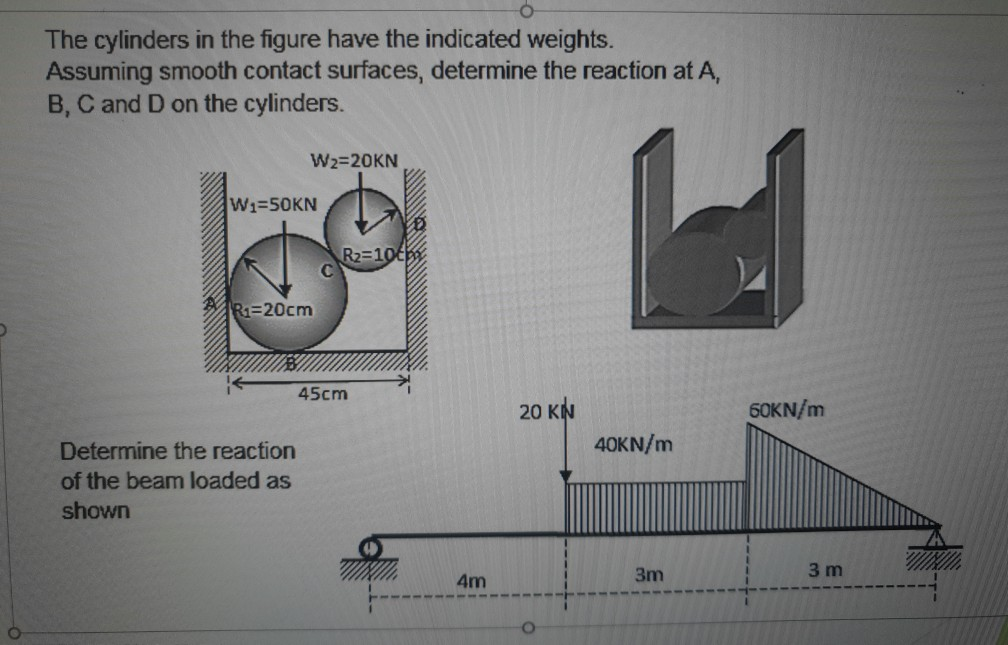
Solved The cylinders in the figure have the indicated
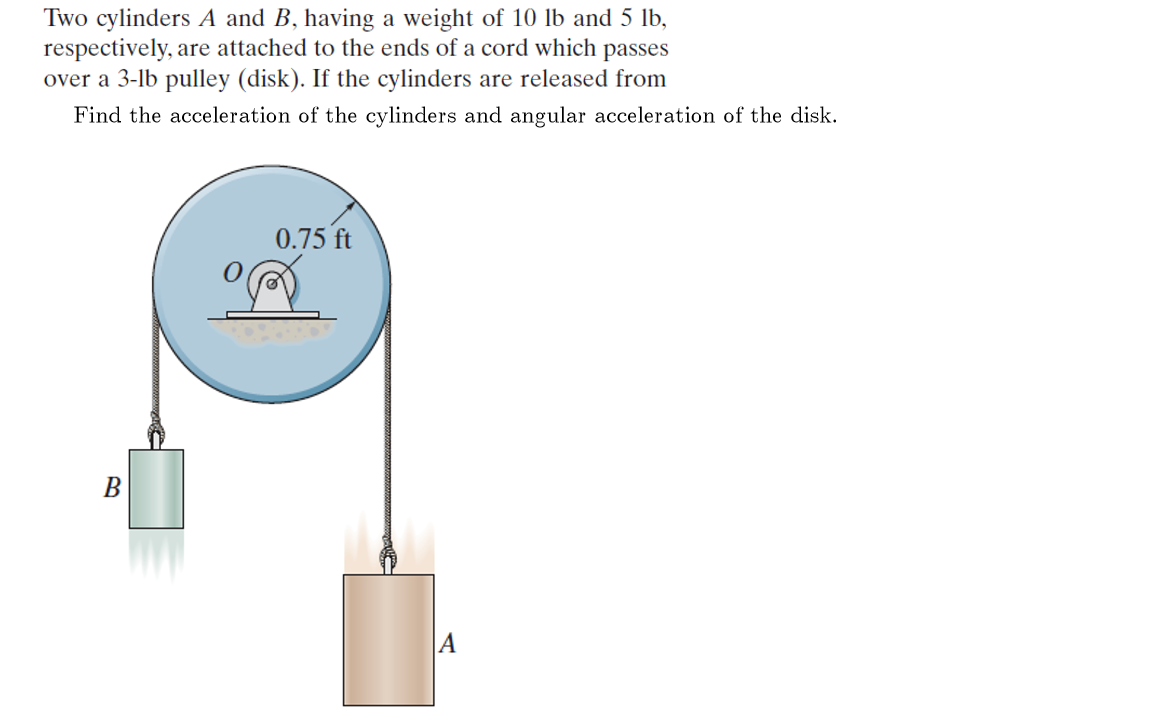
Solved Two cylinders A and B, having a weight of 10 lb and 5
Solved The diagram shows two mathematically similar vases, [algebra] Gauthmath
To find the volume of cylinder B, we can use the concept of mathematical similarity. Since the cylinders are mathematically similar, their corresponding sides are proportional. The formula for the volume of a cylinder is V = πr2h, where r is the radius and h is the height.. Similar solids have the same shape but differ in size, implying that corresponding dimensions are proportional and corresponding faces of the solid are similar polygons.. In the below figures the two cylinders will be similar if the ratios of their corresponding radii and heights are the same. Similarly, the two cubes will be similar if the ratio of their corresponding side lengths is the same.

